TL;DR
Rotating each page to straighten still take a minute with the measuring tool, which can be fiddly, and require zooming deep into the image if we want high accuracy. We can automate this part by computing what the best image rotation angle is down to 0.01°. To that end, Dory has a script to do just that.
Update 2023-12-28: We now have a new version of the script that uses the CUDA enabled OpenCV python library instead of the default CPU one. It can now test angles in increments of .001 degrees and takes a minute per page on a 3060ti. The easiest way to get the OpenCV library with CUDA is to find a pre-built wheel. Make sure to get both the Nvidia GPU Computing Toolkit and cuDNN in the right versions for your wheel.
The output can be plug into Photoshop's Image → Image Rotation → Arbitrary box, or chained into other scripts to automatically rotate the images (e.g. ImageMagick or GIMP's script-fu).
But why? A page crooked by 0.05° surely wouldn't be noticeable right?
Not immediately to the viewer, but to a manga editor who has to redraw around screentones, a perfectly straight page makes cloning gradient screentones (and cloning in general) a heck lot easier.
Imagine having an SFX crossing a vertical panel border, or a vertical pillar in the scene. If the page is perfectly straight, simply making sure the clone tool has Δx = 0 will ensure a seamless clone. Whereas if the page is not straight, having to hunt down where the transition point is and cloning it means lots of work; sometimes that point isn't even in the scene.
Additionally, most mangaka, including Namori, has switched over to using digital screentones (with Comic Studio, for example). Those digital screentones have their dots aligned vertically and horizontally. Having a page that is aligned with those means it's a lot easier to redraw e.g. Ayano and Chinatsu's hair, simply by cloning from another spot of the hair with Δy = 0.
Besides, not having to do something manually is nice. Even with Dory's godly scanning hands (I'm kidding!) our pages are still crooked by more than half a degree regularly, as you'll see below.
Technical details

The script requires NumPy, SciKit-Image, SciKit-Signal, and Matplotlib.
Radon transform
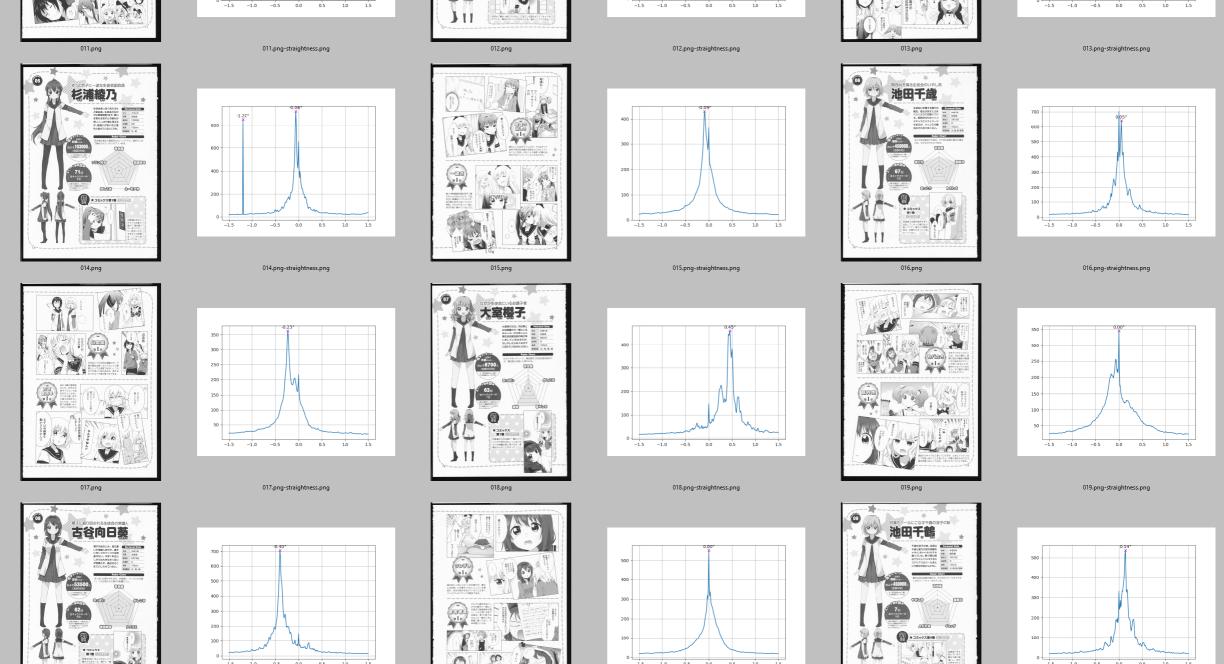
The core of the script is a Radon transformation of the page, which basically projects the image down to a line at different angles.
angles = np.arange(-MAX_ANGLE, MAX_ANGLE + ANGLE_STEP, ANGLE_STEP)
radons = radon(img, angles, circle=False, preserve_range=False)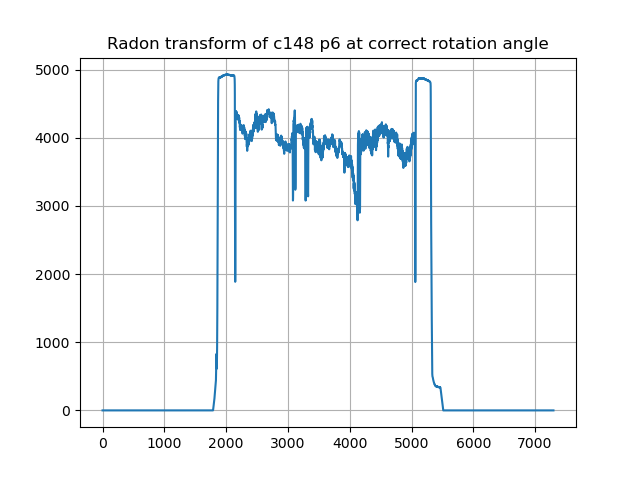
If a manga page is properly rotated, the vertical panel borders will manifest as thin plateau (or in our cases, wells, since they're black against white background) with almost-vertical "walls", with sharp transitions - ideally a step function. A page that is slightly off will have those "walls" slanted when projected down. We can use this to find out how straight the panel borders are in a page against a particular angle. Here's a zoomed-in view of the left panel borders areas of that page, rotated at 0.49° and 0.30° counter-clockwise respectively.
This is the step that takes up the bulk of compute time for this script. For an A5-sized Yuru Yuri page scanned at 600dpi, this step takes around 4 to 5 minutes on a single modern CPU thread.
(You can also notice the two "walls" on the sides of the top graph; those are the white page borders against the black scanner lid)
Second derivative
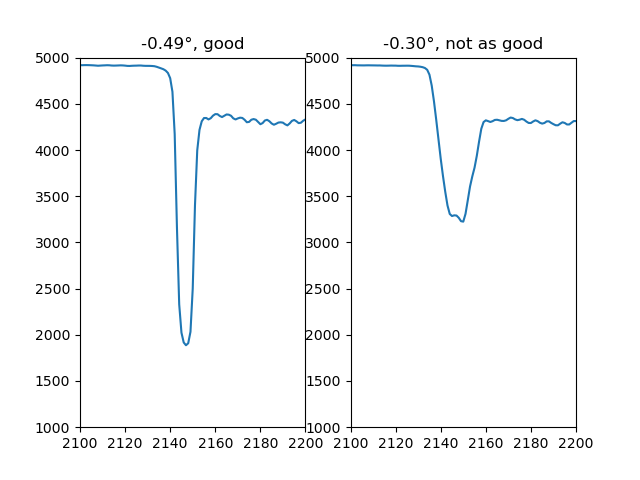
To determine how sharp the panel border transitions are in the radon transformation, we convolve the radon output signal with a Laplacian kernel, basically taking the second-order derivative of the Radon transform. The sharp transitions will result in large impulses in the second derivative signal.
laplacians = [ndimage.laplace(remove_margin(radons[:, i], height, width))
for i in range(angles.size)]
Variance
A simple way to tell how large those impulses are is to take the variance of the second derivative signal (variance is the squared deviation of a signal from its mean). The output is a single number for each rotation angle, signifying how straight our page will be at that angle (which actually has nothing to do with how much yuri is happening on the page).
In our examples, the variance value at -0.49° is 1136, and at -0.30° is only 199. Plotted for the whole rotation range that we're interested in (in our case, we do from -1.5° to 1.5°, since our scans are almost never crooked outside of those ranges).
variances = np.array([np.var(laplacian) for laplacian in laplacians])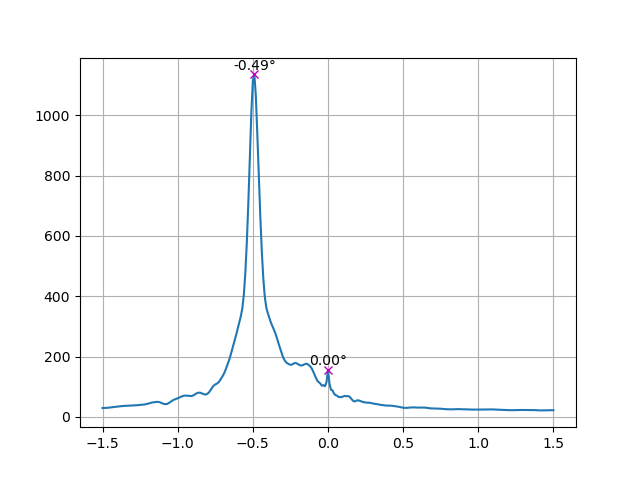
Peaks
Once we have the straightness-vs-angles list, we can find the best angle by looking for the peaks (local maxima) in the straightness signal. Note that the signal is noisy, so some filtering (e.g. peak distance and minimum peak prominence) will be required.
peaks = np.array([])
prominence = PROMINENCE
while peaks.size == 0 and prominence >= 10:
peaks, _ = signal.find_peaks(variances, distance=3,
prominence=prominence)
prominence /= 2
peak_at_zero = [i for i, idx in enumerate(peaks)
if idx == int((angles.size - 1)/2)]
if peak_at_zero and peaks.size > 1:
peaks = np.delete(peaks, peak_at_zero[0])You'll notice that there will almost always be a peak at 0°. This is because the image is a discrete signal; due to the pixel grid, a page not rotated will always be slightly sharper than the same page rotated a little bit. In our script we simply ignored all the peaks at 0° unless there is no other prominent peaks, in which case the image is already straight.
Handling pages with prominent page borders interfering with panel borders
Sometimes the page borders will have a peak that is much more prominent than the panel border peak, if the page has not enough vertical panel walls and sharp edges on both sides. Page 12 of the volume 18 booklet is a good example of this:

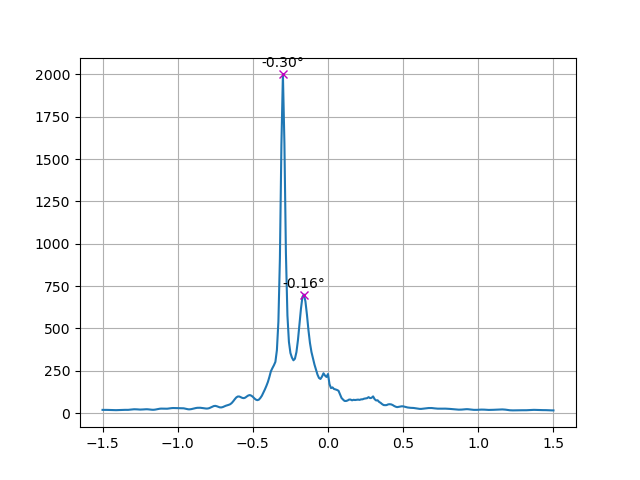
The peak at -0.30° is from the page borders, whereas the peak we want is the one at -0.16°, corresponding to the panel borders. We can avoid this by finding the peaks in the Radon transformation that correspond to the mostly-white page margins and only work with the page content within. Those page margins are generally easy to distinguish.
margin_peaks, _ = signal.find_peaks(
radon_slice, distance=0.7*img_width,
prominence=0.1*img_height, height=0.9*max(radon_slice))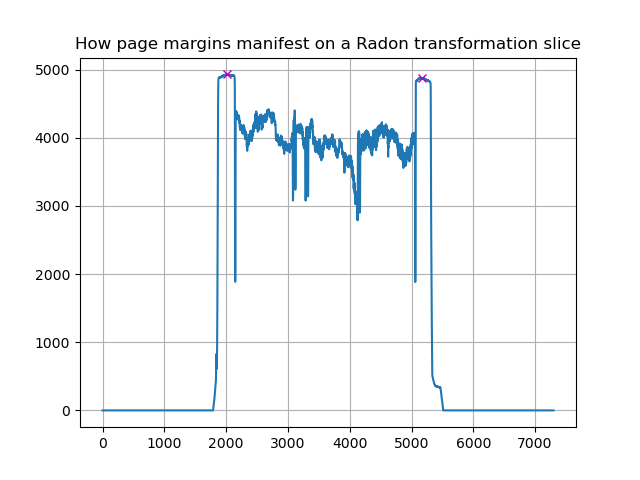
After removing the content outside of the margin, page 12 of volume 18 booklet only has one dominant straightness peak at -0.16° (the page border peak at -0.30° is gone):
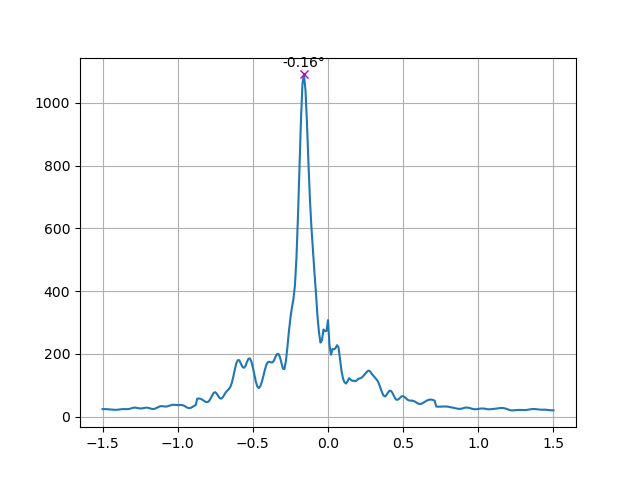
Fixing page skews
To fix page skews (i.e page looking more like a parallelogram than rectangular), we apply the whole process again, but this time on angles around 90° (we do 88.5° - 91.5°) to find the perfect angle to align with horizontal panel borders, then just subtract that from the vertical rotation angle to find the perfect skew angle.
All in all, this can be part of the scanning pipeline, and along with other automated cleaning steps (Photoshop Actions/GIMP scripts) can reduce manga cleaning down to the most boring and the most interesting tasks: dusting and redrawing.